

Человека с давних пор влекло в небо. Иногда это было просто неясной потребностью ощутить себя птицей, попробовать, как это оно там, рядом с облаками. Случалось, что обстоятельства заставляли его задуматься о необходимости оторваться от Земли для того, чтобы преодолеть преграды, возникшие на пути. И хотя довольно часто попытки разорвать путы земного притяжения оказывались неудачными, раз за разом находились новые смельчаки, смело вступившие в спор с гравитацией.
Предлагаемый для учащихся 7-8 классов проект «Воздушный шар» направлен на изучение возможности совершить полёт на летательном аппарате подобного класса по воздуху через препятствие, непреодолимое каким иным способом. На пути могут оказаться непроходимые горы или безбрежный океан, болотистая равнина или суровые ветры, но в каждом конкретном эпизоде нужно оценить реальность и безопасность такого полёта. А для этого придётся выявить и изучить причины, помогающие шару «плыть» по воздуху и научиться предсказывать его поведение в условиях атмосферы и тяготения земли.
Идея проекта – П.Д. Широков
Автор текста – Д.В. Беляев
Под редакцией В.Б. Хозиева
ТОО «Содействие Просвещению»
Центр практической психологии «Февраль», Москва – Сургут, 1995г.
1.1 История Гудвина
«Зовут меня Джеймс Гудвин. Родился я в Канзасе… В молодости я был актёром, играл царей и героев. Убедившись, что занятие даёт мало денег, я стал баллонистом… Я поднимался на баллоне, то есть воздушном шаре, наполненном лёгким газом. Я это делал для потехи толпы, разъезжая по ярмаркам. Свой баллон я всегда привязывал верёвкой. Однажды верёвка оборвалась, мой баллон подхватило ураганом, и он помчался неведомо куда. Я летел целые сутки, пронёсся над пустыней и огромными горами и опустился в стране, которую теперь называют страной Гудвина.
…Я убедился, что из этой страны можно выбраться только по воздуху. Как только я это понял, в голове у меня стали возникать один за другим много вопросов. Раз я сюда долетел на воздушном шаре – на нём же можно и спастись. Но позвольте, кто тогда может сказать мне: вернусь я домой или меня унесёт ещё дальше. Я помню, как ураганный ветер нёс меня над горами, и мой шар чудом не разбился. Ладно, пусть я поймаю нужный ветер и удачно преодолею горы. Но дальше идёт большая пустыня, посадка на которую не менее опасна, чем полёт над горами. К тому же при падении я сильно повредил свой баллон, и мне придётся поставить на него много заплат. Материал, который я здесь раздобыл, очень прочен и не пропускает газ. Плохо то, что этот материал раза в два тяжелее той ткани, из которой сделан мой шар, такие заплаты сделают мой баллон значительно тяжелее, и неизвестно, смогу ли я вообще подняться в воздух. В самом худшем случае мне придётся целиком переделать воздушный шар, и тогда я уже вообще не смогу сказать, долечу или нет…»
– Значит, Ваша цель – вернуться домой в Канзас? – спросил Страшила.
– Да, это стало моей мечтой. – А знаете ли Вы, что для этого надлежит сделать? – Я много думал над этим, даже составил план действий. Но беда в том, что мне не с кем его обсудить. И я был бы признателен любому, кто указал бы на его слабые места.
– Дорогой Гудвин, – радостно воскликнул Страшила, – хоть я и не понимаю ничего в летательных аппаратах, но, по-моему, это неплохой случай проверить, на что годятся мои новые мозги. Я готов помочь Вам в решении этой проблемы, выступая одновременно и как Ваш коллега, и как Ваш критик.
(*) Иногда в тексте Вам будут встречаться таинственные знаки. Не пугайтесь! Это – ваши верные помощники. Каждый из них как бы подсказывает, что курсивный текст за ним: (*) – комментарий, помощь, подсказка; (!) – небольшая исследовательская задача, которую любознательный читатель должен решить либо дома, либо в библиотеке; (?) – задача, которая позволит подробнее разобраться в тех открытиях, которые Вы сделаете.
(!) Вспомните литературные произведения и исторические источники, где упоминается об использовании воздушных шаров. Используйте найденные факты для ответов на вопросы:
1.2 Уточнение постановки задачи.
– Позвольте, я изложу Вам ход моих рассуждений, – продолжал Гудвин. – Прежде всего, я решил поставить задачу более точно. Я взял лист бумаги и, вспомнив всё, что происходило со мной и моим шаром во время урагана, нарисовал примерно следующее (рис. 1).
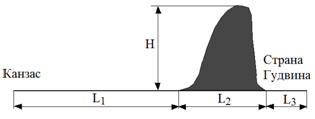
Этот план, как показалось мне, является хорошей моделью местности, над которой предстоит пролететь. На нём схематично изображены горы, выше которых должен подняться мой воздушный шар, и пустыня, которую надо преодолеть.
– Постановка задачи стала немного проясняться, – заметил Страшила. – Если я правильно понимаю, Вам надо построить такой воздушный шар, который мог бы подняться над горами. Но что произойдёт, если в сторону гор будет дуть сильный ветер? Не разобьётся ли ваш летательный аппарат о скалы? Мне кажется, что необходимо учитывать расстояние до гор, скорость ветра и скорость подъёма шара. Вероятно, задачу следует переформулировать следующим образом: с какого минимального расстояния L3 надо взлететь, чтобы не столкнуться с горами?
– Расстояние до гор мы определить сможем, высота гор известна. Наверное, мы как-то сумеем определить скорость ветра (лишь бы не налетел ураган!). Но с какой скоростью взлетает воздушный шар? Я ведь даже не представляю себе, почему они вообще летают! – воскликнул расстроенный Гудвин. – А сколько вопросов, которые я задавал себе, остались без ответа! Вот только некоторые из них. Зависит ли высота подъёма шара от массы снаряжения? Каким газом лучше наполнять оболочку? Можно ли управлять шаром в полёте? В какую погоду лучше всего пускаться в такое рискованное путешествие? Изменятся ли лётные качества шара, когда я поднимусь высоко – выше гор, которые мне предстоит преодолеть. Эти и многие другие вопросы, на которые я не смог ответить, постоянно меня преследуют.
– Дорогой Гудвин! Не стоит отчаиваться. Из всего этого можно сделать лишь один вывод: не следует пускаться в путь до тех пор, пока мы не узнаем всю степень реальности и опасности Вашего предприятия. А для этого, в первую очередь, придётся понять, что всё-таки помогает шару подняться в воздух. Думаю, что это и должно стать нашей самой главной задачей.
(*) У любопытного читателя напрашивается вопрос: как это так, решаем одну задачу, а в постановке их уже две или более? Дело в том, что мы рассматриваем проблему о возвращении Гудвина домой на воздушном шаре. Для нашего героя она оказывается, настолько трудна, что сразу вызывает у него много вопросов. Анализируя их, он вынужденно приходит к новым задачам, решение которых немного приближает его к прояснению общей проблемы. Таким образом, путь героя похож на подъём по лестнице со ступеньками, которые надо пройти друг за другом последовательно, чтобы подняться наверх. Более опытные двигаются наверх, перешагивая через некоторые ступеньки. Пропущенные ступеньки – это те подзадачи, которые считаются уже решёнными и не вызывают особых затруднений.
(?) Давайте и мы, ещё раз послушав размышления героя, попытаемся выписать «ступеньки» нашей «лестницы».
Что у Вас получилось? Отлично! А теперь сравните с тем, что вышло у Гудвина:
1.3. Где начало того конца?.
– Попробуем разобраться в причине полёта, – начал было Гудвин, но был поспешно прерван Страшилой.
– Однако полётом можно назвать всё, что угодно, – возразил тот, – вот, например, брошенный мяч летит по довольно замысловатой кривой и оказывается на земле. Что заставляет его опускаться? Ведь заметьте, что как бы сильно мы его не бросили, он неминуемо падает вниз. И я, сколько бы ни прыгал, никогда не смогу взлететь! Это и понятно – я не птица и у меня нет крыльев. Птицы машут крыльями, как бы отталкиваясь ими от воздуха или опираясь на него…
– Это верно, мой дорогой друг, однако я ведь летал на воздушном шаре, который притягивается вниз так же, как и любая птица (достаточно проткнуть его оболочку, и он упадёт). Но заметьте, у него нет крыльев и ему нечем, как вы сказали, опираться о воздух. Значит, с полётом воздушного шара связана другая причина. Кстати, похожие явления мы можем наблюдать и в воде: одни тела плавают, оставаясь, всё время на поверхности, другие, как топор, идут ко дну.
– Значит, можно предположить, что есть две причины: одна заставляет тела опускаться к поверхности земли, а другая, напротив, поддерживает их в воздухе? – задумчиво произнёс страшила.
Гудвин обрадовался:
– Вот именно, из всего сказанного следует, что суммарное действие этих факторов и приводит к тому, что у тел появляется способность летать или плавать, если речь идёт о жидкостях. И наша с Вами задача – попытаться определить те характеристики тел, которые отвечают за это удивительное свойство.
– Мне кажется, что этого недостаточно. Вы же сами сказали, что разные тела обладают разной «летучестью» (или «плавучестью»), и именно от этого зависит успех Вашего перелёта. А значит, нам надо научиться измерять величину воздействия среды на наш шар и, исходя из этого, пытаться угадать возможную траекторию полёта относительно гор. Так, как нам ничего не известно об этом явлении, нам лишь остаётся наблюдать за различными телами, погружая их в разные среды, и на основе происходящего делать выводы, то есть ставить эксперименты.
1.4. Об экспериментах.
– Я совсем запутался, – начал Страшила, – хотя сначала ситуация вроде бы прояснилась. Мы берём тело, погружаем его в среду и смотрим, что из этого выйдет. Вроде всё просто. Однако как оценить полученный результат и сделать правильные выводы? Я привык делать выводы на основе каких-либо предположений, догадок о происходящем.
– Я тоже думал об этом, – задумчиво произнёс Гудвин, – и мне пришла в голову одна мысль. Давай попытаемся понять, насколько она ценная. Вот послушай. Выполнению какой-либо работы предшествует некоторая причина, из-за которой всё затевается. Эта причина и является ЦЕЛЬЮ, которую мы пытаемся достичь, её ещё можно назвать КОНЕЧНЫМ РЕЗУЛЬТАТОМ. Так бывает всегда, строим ли мы воздушный шар или дом. Любая исследовательская работа тоже не исключение. Её целью служит проверка некоторого предположения или догадки, точнее, не их самих, а их справедливости. Исследователь, проводящий работу, ожидает, что некоторый исход опыта должен либо подтвердить его предположение, либо это предположение опровергнуть. Этот исход и является развязкой, ради которой весь эксперимент и затевался.
– Может быть, это и так, – засомневался Страшила, – однако КОНЕЧНЫЙ РЕЗУЛЬТАТ, несомненно, зависит от способа проведения эксперимента. Где гарантии того, что этот результат является следствием именно исследуемого нами явления? Но и это ещё не всё. Вы говорили, что выводы делаются на основе ожидаемого КОНЕЧНОГО РЕЗУЛЬТАТА. Но как я могу чего-либо ожидать, если я толком ничего не знаю об исследуемом явлении?
– Не торопись, любезный Страшила, – улыбнулся Гудвин. – Во многих экспериментах возможные результаты определяются достаточно просто. Например, погружая тело в воду, ты из личного опыта можешь сказать, что оно либо утонет, либо всплывёт на поверхность. Это и есть ожидаемые КОНЕЧНЫЕ РЕЗУЛЬТАТЫ. Первый же вопрос, который ты мне задал, достаточно важен, и ответ на него зачастую очень сложен. Действительно, проводя эксперименты, мы работаем в основном не с исследуемыми телами, а с их копиями, и надо получить гарантии, что исследуемые свойства копии и объекта совпадают. Иначе говоря, копия должна моделировать исследуемые свойства объекта. Это – важнейшее условие успешного проведения эксперимента. Кроме того, необходимо определить методы наблюдения какого-либо свойства или измерения интересующей нас величины. Если эти свойства (величины) недоступны для непосредственного наблюдения, то важно придумать методы их косвенного определения через доступные для наблюдений и измерений величины и свойства.
– Очень хорошая идея, – сказал после небольшого раздумья Страшила, – и я хочу добавить ещё несколько мыслей. Большинство экспериментов проводится не на самих телах, а на их копиях-моделях, имитирующих значимые свойства. Однако при этом копии-модели, помимо всего прочего, обладают специфическими, присущими только им свойствами, которых нет у исследуемого объекта. Эти и другие соображения приводят к мысли о том, что в ходе эксперимента гарантировано появятся ПОБОЧНЫЕ ЭФФЕКТЫ, что достаточно неприятно.
– Совершенно верно, Страшила, – сказал Гудвин, – всё это, безусловно, встречается практически в любом эксперименте. Всё то, что нами обсуждалось, я хорошенько обдумал и решил кратко записать, сделав при этом некоторые дополнения. Смотри, что получилось:
(*) Эта табличка в дальнейшем поможет Вам самим планировать и проводить эксперименты, направленные на выявление значимых свойств среды и объекта.
(!) Самостоятельно спланируйте и проведите лабораторную работу с целью измерения объёмов твёрдых тел. При этом старайтесь придерживаться той последовательности действий, которая задана в табличке Гудвина.
(*) Если у Вас возникли трудности, то посмотрите, что получилось у Страшилы:
Лабораторная работа
|
N экспер. V, м3 |
1 | 2 | 3 | ... | N | V ср, м3 |
7-9 пункты заполняются во время лабораторной работы и после получения результатов.
(!) Предложите более простой (однако, менее точный) метод измерения объёмов твёрдых тел, используя лишь одну кювету с нанесённой на ней мерной шкалой.
2.1. Немного истории.
Итак, Гудвин и Страшила занялись изучением причин полёта воздушных шаров и возможностью их использования с целью преодоления различных препятствий.
Гудвин изложил Страшиле свои планы:
– Целями наших ближайших исследований должны быть следующие вопросы. Во-первых, необходимо изучить историю воздухоплавания. Это поможет нам разобраться с типом шара, который мы будем строить. Как я уже говорил, водород мы получить сумеем, однако следует ли им заполнять оболочку шара? Для этого оболочку необходимо сделать закрытой, иначе весь водород быстро улетучится. Такие типы шаров, поверь мне, достаточно сложны в изготовлении. С другой стороны, мы можем использовать полученный водород для нагрева воздуха внутри оболочки шара. Это проще с конструктивной точки зрения, однако, количество требуемого водорода значительно увеличится. Такие типы шаров называют монгольфьерами. Так же не мешало бы выяснить возможности основных типов шаров: нет смысла строить шар, который заведомо не перелетит через гору. Во-вторых, следует установить ряд законов, по которым летают воздушные шары. Для этого надо будет, обзавестись некоторым простейшим оборудованием, провести ряд экспериментов. Эти эксперименты я разбил на три типа:
– Насколько я Вас понял, – протянул Страшила, – надо идти в библиотеку и читать разные умные книжки о воздушных шарах?
Гудвин прервал его:
– Не просто читать, а стараться узнать из книг что-то новое, полезное для себя. Интересные с твоей точки зрения факты желательно записывать в специально выделенную для работы тетрадку, иначе ты их просто забудешь.
Страшила пошёл в библиотеку и нашёл несколько книг на изучаемую тему.
Из тетради Страшилы:
Чертежи трёх летательных машин, парашюта, геликоптера и крылатого аппарата были найдены в рукописях Леонардо да Винчи, живущего в конце XV века.
Воздушные шары были изобретены в XVIII веке; 5 июня 1783 года во Франции, в городе Анноне, с городской площади впервые поднялся воздушный шар, наполненный горячим воздухом. Его изобрели и построили братья Ж. и Э. Монгольфье, а первыми аэронавтами были петух и баран. С тех пор воздушные шары с открытой оболочкой, наполненной горячим воздухом, стали называть монгольфьерами.
21 ноября 1783 года в Париже состоялся первый полёт людей: аэронавты Пилатр де Ролье и д'Арланд пробыли в воздухе 25 минут, поднявшись на высоту около 1000 метров.
Управляемый полёт. В 1852 году изобретатель А. Жиффар построил сигарообразный аппарат (дирижабль) с гребным винтом, приводившимся во вращение небольшой паровой машиной. Однако массовое строительство дирижаблей смогло начаться лишь после изобретения мощного и лёгкого двигателя внутреннего сгорания. Первый такой двигатель был создан в конце 80-х годов XIX века, а в ноябре 1898 года француз А. Сантос-Дюмон на дирижабле своей конструкции облетел вокруг Эйфелевой башни. Дирижабли наполняли водородом и гелием, они были громоздки, неуклюжи и тихоходны.
Гудвина не удовлетворила работа Страшилы:
– Это интересная историческая справка, – сказал он. – Однако здесь ничего не сказано об основных типах воздушных шаров и их характеристиках: максимальной высоте и дальности полёта, грузоподъёмности, материале, из которого был шар изготовлен. Кроме того, ничего не сказано о построении модели воздушного шара.
(*) Постарайтесь найти эту информацию в библиотеке.
2.2. О натуральной модели шара.
В ходе работы над решением поставленной проблемы наши герои решили заключительную часть исследований проводить с помощью натурной модели воздушного шара.
– Натурное моделирование, – объяснял Гудвин Страшиле, – это исследование объектов и их свойств на моделях-прототипах, подобных настоящему предмету. Такая модель воспроизводит конструкцию и действие (включая взаимодействие со средой) своего образца. Обычно натурные модели бывают меньших размеров, чем исследуемый объект. Правда, бывают случаи, когда их размеры совпадают или превосходят размеры оригинала.
Подумав немного, Страшила спросил:
– Как же мы будем проводить исследования с моделью воздушного шара, если он настолько мал, что даже поодиночке мы не сможем забраться в его корзину? Получается, что все эти модели не более чем игрушки, пригодные лишь для развлечения.
– Слушай дальше, нетерпеливый Страшила, – улыбнулся Гудвин, – и ты поймёшь, в чём тут дело. Нам ни к чему садиться в корзину нашей модели. Одна из целей моделирования – получение данных, помогающих оценить реальные нагрузки, действующие на шар и его характеристики. Мы будем исследовать нашу модель почти в тех же условиях, в которые затем попадёт реальный шар. Такое моделирование поможет нам наглядно увидеть будущую конструкцию и проверить её действие.
– Я не о том, – не унимался Страшила. – Почему Вы считаете, что такая модель достаточно точно опишет всё, что будет происходить и с реальным воздушным шаром?
Гудвин продолжил:
– Вопрос, который ты задал, очень важен при проведении любых натурных экспериментов с моделями объектов. Для того, чтобы сведения, получаемые в ходе эксперимента, можно было распространить на настоящий шар, надо соблюсти несколько условий. Одно из них – достаточно точное подобие оригинала: модель желательно делать из того же материала, что и будущая конструкция; в ней должен быть так же распределён вес между деталями, как и в реальной конструкции; должно точно соблюдаться отношение размеров отдельных деталей. Другим важным условием можно считать устранение всех посторонних факторов, возникающих в ходе эксперимента и способных в существенной степени повлиять на его исход.
3.1. Свойство «быть тяжелее, чем…»
Итак, наши герои приступают к исследованию способности тел плавать в воздушном пространстве. Для этого они хотят использовать метод «по аналогии», рассматривая вместо газообразной среды жидкость. Последнее значительно упрощает работу, так как многие тела, доступные для исследования, сделаны из веществ как плавающих в жидкости, так и тонущих в ней, что легко определимо при эксперименте.
– Когда практически ничего не известно об исследуемом явлении, – начал Гудвин, – надо попытаться связать его с какими-то уже изученными свойствами веществ или явлений. В нашем случае надо постараться подобрать некоторую качественную характеристику тела, непосредственно влияющую на его свойство «плавать».
– Мне кажется, всё просто, – сказал Страшила. – Я считаю, что значимой характеристикой для свойства «плавать» может служить масса тел. Вот посмотрите: лёгкое дерево плавает в воде, однако тяжёлая железная болванка сразу утонет. Я прав?
– Не уверен, – ответил Гудвин. – В свою очередь я могу привести пример, опровергающий твоё предположение. Возьмём большой деревянный брусок и железный гвоздь. Можно подобрать брусок так, что его масса будет во много раз превышать массу гвоздя. При этом гвоздь тонет, а брусок плавает.
– Да, Вы правы, – расстроился Страшила. – Но ведь железо намного тяжелее дерева. И если масса тел не влияет на свойство плавать, то я больше ничего не могу придумать.
– Не расстраивайся, Страшила, – стал успокаивать его Гудвин. – В своём рассуждении ты, мне кажется, практически вплотную подошёл к разгадке. Когда ты говорил, то употреблял термины «тяжесть» и «масса». Первый из них чаще всего используется в разговорной речи. Говорят: «один предмет тяжелее другого», используя его на интуитивном уровне. Термин «масса» определяет некоторую количественную характеристику тел; за ним стоит некоторая величина, которую можно измерить. Предлагаю на некоторое время перейти на уровень интуиции и обсудить значимость свойства «тяжесть» подробнее. Точнее, я бы сказал, мы будем использовать свойство «быть тяжелее, чем…», относящееся уже не к одному, а к паре тел.
– Не совсем понимаю, для чего это нужно? – удивился Страшила. – Вы ведь показали, что это свойство не является значимой характеристикой для свойства «плавать». Зачем же к нему ещё раз возвращаться?
– всё просто, – продолжил Гудвин. – Плавает всё, что «легче», а тонет всё, что «тяжелее». Это очень туманное рассуждение, но с ним трудно не согласиться. Оно станет яснее, если рассматривать предметы одинаковой геометрической формы и размера…
– Начинаю немного понимать, – обрадовал его Страшила, – при этом, очевидно, железное тело будет тяжелее деревянного. И Вы считаете, что в этом случае всё должно встать на свои места?
– Может быть, – задумался Гудвин. – Не мешало бы это проверить. Надо провести эксперимент.
– Давайте его планировать, – загорелся Страшила и полез в карман за своим конспектом. – Пункт первый: цели работы…
Страшила стал писать:
– Уф, закончил, – Страшила довольно посмотрел на Гудвина.
– Отлично, – похвалил его Гудвин. – Можно начинать. Только записи надо вести предельно аккуратно. Они необходимы для подведения итогов и выводов.
И наши герои приступили к экспериментированию.
(*) Выполните лабораторную работу №1 и сравните свои выводы с выводами Гудвина и Страшилы.
После работы в конспекте Страшилы появилось ещё несколько пунктов:
– Для тел одинакового вида (размера и формы) всё ясно, – промолвил Страшила, – но что это означает? Когда мы накладываем ограничение на рассматриваемые тела, то свойство «тяжесть» значимое, а когда рассматриваем произвольные тела – нет. Что-то уж очень запутанно.
– Вовсе нет, – ответил Гудвин. – Для произвольных тел эту характеристику тоже можно считать значимой, однако проследить эту зависимость значительно труднее. Здесь мы рассмотрели только частный случай, который помог нам это выявить. Мы зафиксировали некоторую характеристику тела и, выбросив её из рассмотрения, получили результат. Однако скажи, зафиксировав форму и размеры тел, что мы тем самым сделали неизменным?
3.2. Связь массы тела с его объёмом.
Страшила долго думал, но, в конце концов, пришёл к мысли, что это был объём. Об этом он и сказал Гудвину.
– Верно, – подтвердил тот, – все наши тела обладали равным объёмом. В этом легко убедиться, проведя соответствующие измерения, делать которые мы умеем.
– Получается, что мы не знаем точно, как на свойство тел плавать влияет изменение их объёма, – заметил Страшила.
– Да, однако, мы обладаем рядом наблюдений, которые позволяют продолжить рассуждения. Смотри: из наших опытов получается, что если бы мы имели в распоряжении тело, массу которого можно было бы изменять, не изменяя при этом объёма, то с ростом массы это тело в некоторый момент времени перестало бы плавать. Однако тел, обладающих таким свойством, скорее всего не существует. Поэтому хорошо было бы найти закон изменения массы тела в зависимости от его объёма. Выразив, таким образом, массу через объём, мы бы смогли в дальнейшем пользоваться лишь величиной объёма тела (или массы), что разрешило бы вопрос о значимости характеристики «тяжесть» для тел произвольной формы и размера.
– Да, – ответил Страшила, – эта зависимость нам бы сейчас вовсе не помешала. Но как её найти? Я ещё ни разу не искал зависимостей. А вдруг её вообще не существует.
– Опять же не всё потеряно, – ответил Гудвин. – Есть ряд методов, используя которые можно устанавливать неизвестные соотношения. Тот из них, который я собираюсь применить, является отчасти экспериментальным. Однако в данном эксперименте очень важным этапом будет обработка полученных данных. Умение наглядно представить результаты эксперимента особенно важно при попытках обнаружить неизвестные закономерности или соотношения. В частности, одним из таких способов представления результатов является построение графика методом координат…
Страшила не имел ни малейшего представления о каких-либо графиках и о том, как их строят, поэтому он сразу открыл свой конспект и начал записывать.
(*) Выясните, в чём заключается метод координат. Что такое координаты точки и как поставить точку, зная её координаты. Как в системе координат можно таблично задать отрезок, луч и прямую.
– Теперь можно планировать эксперимент, – закончив писать и отложив конспект, сказал Страшила. – Но меня мучает ещё один вопрос: как сформулировать то, что мы хотим получить, то есть ожидаемый результат?
– Я считаю, что ожидаемым результатом этой работы можно считать наличие или отсутствие зависимости. Действительно, трудно что-либо предполагать о её виде в нашем положении.
Страшила снова взялся писать. Опыта у него прибавилось, поэтому он справился с работой значительно быстрее.
(*) Выполните лабораторную работу №2 и сравните свои выводы с выводами Гудвина и Страшилы.
Заполнив таблицу и нанеся на график экспериментальные точки для набора тел, сделанных из железа, Страшила получил следующее (рис. 2)
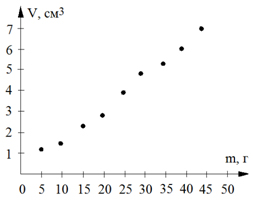
Он вопросительно посмотрел на Гудвина.
– Отлично, – похвалил его тот. – Теперь внимательно посмотри на то, что получилось, и попытайся прийти к какому-нибудь заключению.
После недолгих раздумий Страшила взял чертёж и соединил на нём некоторые точки (рис. 3).
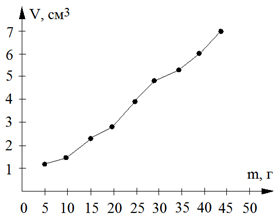
– Если соединить точки последовательно, – сказал он, – то получится ломаная. Честно говоря, это мне ни о чём не говорит. Скорее всего, мы где-то ошиблись.
– Может и так, – сказал Гудвин задумчиво. – Но мне кажется, что наши ошибки носят особый характер. Насколько я понял, ты имеешь в виду ошибки в планировании и проведении эксперимента. Я же полагаю, что таковых просто не было. Всё дело в том, что любой эксперимент, так или иначе связанный с измерением чего-либо в ходе его проведения, обречён на кучу ошибок. Это связано с тем, что любой измерительный инструмент неточен и даёт погрешности в измерении. Вот смотри, мензурка, которой мы измеряли объём вытесненной жидкости, градуирована с интервалом 0,1 миллилитра, а это означает, что объём в 0,01 миллилитра с помощью этой мензурки мы уже отмерить не сможем. Точность инструментов со шкалами (линейки, мензурки, весы и т.д.) считается равной половине цены деления шкалы…
(*) Подробнее о погрешностях при проведении измерений величин можно узнать из учебника физики. Прочитайте эту главу. Уделите особое внимание вопросу о построении графиков кривых по экспериментальным таблицам с учётом погрешностей.
Учтя погрешности измерений, Страшила не без помощи Гудвина получил график экспериментальной кривой (рис. 4).
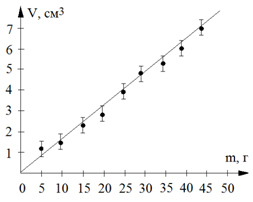
– Что получилось? – задал вопрос Гудвин. – Как что? – удивился Страшила. – Прямая получилась. Прямая, выходящая из начала координат. Хотя я не совсем понял, почему мы провели прямую, а не какую-нибудь иную кривую, проходящую через экспериментальные точки?
– Всё просто, – продолжил Гудвин. – Сам посуди: линейный закон наиболее естественно описывает процесс увеличения массы с ростом объёма, а кроме того, прямая – самый простой вид кривых, удовлетворяющих точкам графика. К тому же если провести через экспериментальные точки вертикальные линии, то они будут отсекать подобные треугольники. Из их подобия следует соотношение
m1/V1 = m2/V2 = … = mN/VN = const
для каждого из наборов тел. Отсюда следует предположение, что для любого твёрдого тела, сделанного из определённого вещества, отношение его массы к объёму есть величина постоянная. Эту величину назвали плотностью данного вещества (ρ).
(*) Посмотрите параграф о плотности веществ в учебнике физики. Найдите по таблицам плотности веществ, из которых были сделаны использованные в лабораторных работах тела. Сравните эти величины с получившимися в ходе лабораторной работы значениями. Лежат ли они в допустимых интервалах, связанных с погрешностями измерений? Сделайте выводы. Понятие плотности может относиться и к телу. В частности, если оно целиком состоит из одного вещества, то его плотность и будет плотностью этого вещества. Это очевидно. Чаще же тела состоят из нескольких веществ. Поэтому их плотность отличается от плотностей веществ, составляющих части этих тел. Она всегда лежит где-то между плотностями наиболее и наименее плотной из компонент. Пусть тело состоит из n частей. Каждая часть обладает объёмом Vi и массой mi. Тогда плотность всего тела будет равнаρср = Σ ρiVi / Σ Vi
Величина ρср, стоящая слева в этой формуле, носит название средней плотности тела. Эта зависимость очень важна, так как воздушные шары обычно изготавливаются из различных материалов с различными плотностями.
(?) 1. Выведите эту формулу или посмотрите её вывод в учебнике физики.
2. Составляя тело из компонент, одни из которых тонут в воде, а другие остаются на плаву, можно добиться того, что тело не будет ни тонуть, ни всплывать, а останется на той глубине, на которой оно было отпущено. Исследуйте это свойство, используя в качестве веществ пенопласт и пластилин.
3.3. Пара плотностей.
– Подведём промежуточные итоги, – посмотрел на Страшилу Гудвин.
– Хорошо, – начал Страшила. – Значит, из того, что мы получили в ходе экспериментов, следует очень важный вывод: свойство тел плавать зависит от их «тяжести» – интуитивном понятии, которое, однако, хорошо согласуется с массой тел. Последнее было подтверждено для исследуемых тел с равным объёмом. Затем мы задались вопросом о связи между массой тел и их объёмами – оказалось, в виде линейной зависимости с коэффициентом, называемым плотностью вещества, из которого эти вещества состоят. Можно предположить, что именно эта характеристика и влияет на способность тел держаться на воде. Остаётся, правда ещё один параметр – объём тела, влияние которого ещё надо исследовать, но на первый взгляд его роль в плавании тел стоит под большим сомнением.
– Может и так, – подтвердил Гудвин. – Но, пожалуйста, объясни: почему ты так решил?
– Всё просто. Вот смотрите. Большое деревянное полено плавает не хуже, чем маленький брусок из того же дерева, – стал объяснять Страшила.
– Но это ещё ничего не значит, – усомнился Гудвин. – Может быть, для каждого материала можно подобрать некоторый объём, начиная с которого тела, сделанные из него, будут тонуть?
– Не думаю, – продолжил Страшила. – И вот почему. Я заметил следующее: когда мы погружаем тело в жидкость, то отношение объёмов его частей (той, что под водой, и той, что над водой) не изменяется для тел, сделанных из одного материала.
(?) Прав ли Страшила? Спланируйте и проведите эксперимент, подтверждающий или опровергающий слова Страшилы. После работы обсудите с товарищами следующий вопрос: является ли объём тела значимой характеристикой для способности тел плавать?
– Молодец, Страшила, – похвалил его Гудвин. – Это очень важное наблюдение. Но позволь и мне сделать одно замечание. Мы так увлеклись изучением свойств объекта, что оставили без внимания ещё одну важную составляющую, без которой невозможно обойтись. Это среда, в которой находятся наши тела. Фактически она – такой же объект для исследования, как и все рассмотренные нами тела. Давай возьмём кубик льда. Лёд плавает в воде. Однако если поместить его, скажем, в растительное масло, то он утонет. В ходе эксперимента наше тело практически не изменилось. (Эксперимент надо проводить достаточно быстро, так как лёд начинает сразу таять). Значит, на свойство тел плавать влияет также и то, в какой среде мы рассматриваем наше тело.
– Следовательно, необходимо выяснить, какие параметры среды влияют на свойство тел плавать в ней, – задумался Страшила. – То есть надо повторить все лабораторные работы сначала, только всё внимание обратить на вещество, выступающее в роли среды?
– Можно и так, – продолжил Гудвин. – Однако это – очень долгий путь. Стоит его укоротить, вспомнив, что мы исследовали. Во-первых, можно сразу отбросить такие параметры среды, как объём и масса. Об этом нам говорят только что приведённые тобой рассуждения о значимости объёма для плавания тел. Отношения объёмов надводной и подводной части постоянно. Эта величина также не зависит от размера и формы сосуда, в котором мы проводили эксперимент (лишь бы этот сосуд был достаточно широким и глубоким, чтобы тело не касалось его стенок и дна).
(?) Убедитесь в этом самостоятельно. Особое внимание необходимо уделить плотности вещества, из которого состоит среда в эксперименте.
(*) Спланируйте и проведите лабораторную работу, целью которой является экспериментальное определение плотности жидкости. В качестве жидкостей исследуйте воду, масло, глицерин.
– Очень просто, – не унывал Страшила, – проведём эксперимент и посмотрим, так ли это на самом деле.
– Хорошо, давай вместе продумаем его ход. Ведь у нас уже будет иметься не одна плотность, а пара плотностей. В ходе работы уже возникнет какая-то связь между ними? Только вот её вид мне не совсем понятен.
– Предлагаю, надо просто записывать плотности пар веществ, участвующих в эксперименте, и наблюдения за плаванием тела, а затем. Исходя из результата и построив график, подобрать зависимость. Подойдёт? – предложил Страшила.
– Великолепно! – подхватил его Гудвин. – Начинай.
Из конспекта Страшилы:
– Всё просто, – посмотрел на таблицу с результатами Страшила. – Сразу видно: если плотность вещества меньше плотности жидкости, то тело плавает, в противном случае оно тонет. Здесь и график-то никакой не нужен.
– Верно, – подтвердил Гудвин. – Для этого заключения достаточно лишь хорошо составленной таблицы. Как же описать математически только что полученный результат?
– У меня есть идея! – гордо заявил Страшила. – Надо вычесть из плотности среды плотность тела. Если при этом получается положительное число, то тело плавает, если отрицательное – тонет. Всё дело в знаке разности!
– Великолепно, Страшила, со временем ты начал замечать очень интересные вещи. У меня тоже родилась идея. Если разделить плотность тела на плотность среды, то получится число, по величине которого тоже можно судить о способности тела плавать. Если полученная величина меньше 1, то тело плавает, а если больше – тонет. Однако твоя идея мне больше нравится. При расчётах проще оперировать со знаками, нежели сравнивать величины друг с другом.
(*) Гудвин предложил следующий способ измерения плотности воды: «Можно растворить в ней обыкновенную поваренную соль: плотность кристаллов соли больше плотности воды (почему он так решил?), их объём достаточно мал, значит, при растворении соли в воде плотность последней должна возрасти». Проверьте это рассуждение экспериментально. Затем посмотрите, как с этим справился сам Гудвин.
Из записей Гудвина:
«Облепив пластилином кусочек пенопласта, я добился того, что моё тело находилось в состоянии покоя на любой глубине, т.е. его средняя плотность стала равна плотности воды. Затем я прилепил к нему ещё небольшой кусочек пластилина. Так что оно медленно пошло ко дну. Последнее говорит о том, что средняя плотность тела немного возросла. Растворяя в воде поваренную соль, мне удалось заставить тело всплыть на поверхность. Учитывая массу дополнительного кусочка пластилина, я рассчитал, что плотность раствора поваренной соли превысила 1,05 г/см3. Однако, как я убедился, этот показатель можно значительно превзойти.
(?) Определите экспериментально, по примеру Гудвина, максимально возможную плотность соляного раствора в воде.
3.4. Способность поднимать груз..
Страшила был удовлетворён проделанной работой, однако оставался ещё ряд нерешённых вопросов, которые не давали ему покоя.
– Определять, всплывёт тело или нет, мы уже научились, – задумчиво произнёс он. – Но вот что по-прежнему непонятно: если тела плавают вне зависимости от объёма, зачем же делать таким большим воздушный шар?
– Страшила, – обратился к нему Гудвин, – этот вопрос мы, по-моему, уже обсудили. Может, это прозвучало и не очень чётко, но речь о нём шла, когда мы говорили о средней плотности тел. Как ты знаешь, воздушные шары имеют достаточно сложную конструкцию: это и оболочка, и корзина, и стропы, и многое другое. Оболочка наполнена лёгким газом или горячим воздухом. Все эти части имеют различные плотности. Лишь плотность содержимого оболочки легче плотности окружающей среды – воздуха. Как ты понял, чтобы шар мог лететь, средняя плотность всей конструкции должна быть меньше плотности воздуха. Этого можно достичь за счёт увеличения объёма лёгкого газа. Пусть V1 и ρ1 – объём и средняя плотность конструкций шара, а V2 и ρ2 – объём и плотность газа в оболочке, тогда
ρ = (ρ1V1+ρ2V2)/(V1+V2).
Тогда с ростом V2 при постоянном V1 средняя плотность всего воздушного шара будет уменьшаться, приближаясь к ρ2. А это значит, что начиная с некоторого значения этого объёма, средняя плотность шара станет меньше плотности воздуха, и он полетит. Понятно?
– Да, – ответил Страшила. – Однако аналогично можно поступить и с поднимаемой массой. Ведь если взять шар с постоянным объёмом оболочки, то добиться его взлёта можно ещё уменьшением массы конструкции.
– Именно так, – продолжил Гудвин. – Обозначим за M (массу конструкции шара) величину V1 ρ1. Тогда,
ρ = (M+ρ2V2)/V2
– Постойте! – воскликнул Страшила. – Вы забыли объём V1 в знаменателе дроби!
– Я только собирался об этом сказать, – успокоил его Гудвин. – Видишь ли, объём шара V2 настолько велик, что в нашем случае, при приближённых расчётах, объёмом конструкции V1 можно пренебречь.
(?) Оцените погрешность такого приближения. Надеюсь, сомнений в допустимости этого приближения нет? Отлично. Как уже мы говорили, тело летит, если его средняя плотность меньше плотности среды. При равенстве этих плотностей тело не всплывает и не тонет – оно покоится. Эту массу и примем за критическую для данного объёма газа V2, обозначим её Mкр. Пусть плотность среды – ρ0, тогда
(Mкр+ρ2V2)/V2= ρ0.
Откуда
Mкр=(ρ0-ρ2)V2.
– Предлагаю проверить это на практике, – попросил Страшила. – Продолжим исследования в воде?
– Давай ещё раз сделаем это в нашей лаборатории, а затем, если понадобиться, поэкспериментируем с натурной моделью шара.
– Хорошо, – отозвался Страшила и полез за своим конспектом.
Из конспекта Страшилы
Учитывая погрешности, Страшила пришёл к выводу, что полученная Гудвиным формула для критической поднимаемой массы верна. Об этом он поведал Гудвину.
– Используя полученные результаты, уже можно сделать ряд важных заключений о конструкции и размерах шара, на котором мы собираемся лететь. Можно рассчитать его взлётную массу и размеры оболочки, можно оценить и высоту, на которую он поднимется, – сказал Гудвин.
– Как это? – удивился Страшила.
– Достаточно просто, – улыбнулся Гудвин. – Если известны все параметры шара, то его подъём будет продолжаться до тех пор, пока его средняя плотность не сравняется со средней плотностью окружающего его воздуха…
– Простите, а почему, собственно говоря, они должны сравняться? – перебил его рассказ Страшила.
– Это – свойство атмосферы нашей планеты, а также атмосфер всех других планет, где они есть. Насколько я вижу, ты не имеешь никакого понятия об этом, поэтому лучше всего сходить в библиотеку и самому разобраться в этом вопросе.
(*) Найдите в библиотеке материал об атмосферах планет, их составе, свойствах и о том, как меняется плотность воздуха с высотой в земной атмосфере.
– Приступим к постройке модели воздушного шара, – сказал Гудвин. – Это – очень важный этап, так как только на подобной модели мы во всей полноте сможем оценить большинство качественных особенностей летательного аппарата этого типа.
Страшила был очень взволнован словами Гудвина: он уже давно мечтал заняться подобного рода практическими экспериментами. Лабораторные работы с колбами и пробирками ему уже порядочно надоели. Он даже начал немного терять интерес к работе, но как только Гудвин сказал последние слова, глаза его снова радостно засияли.
– Побегу брать нитки и парусину, – радостно крикнул он и уже собрался куда-то идти, но был остановлен Гудвиным:
– Опять ты торопишься. Что ты собираешься делать с этой парусиной?
– Сошью из неё шар, надую лёгким газом и запущу, – без малейшего смущения ответил страшила.
– Гудвин улыбнулся: – Начнём сначала: как ты будешь шить шар?
– Очень просто, – не унимался Страшила. – Я возьму парусину, разрежу её на лоскуты и затем сошью из них шар. У меня получится, я это точно знаю. Один раз я наблюдал работу портного. Он поступает с тканью точно так же.
– И у него получается шар? – Нет, почему? У него получается рубашка или брюки. – А если у тебя получатся брюки? – Гудвин снова улыбнулся: наивность Страшилы его явно занимала. – Не проще ли снять свои и надуть их газом?
Здесь Страшила задумался. Думал он долго. Его мучил вопрос: почему у портного получается именно то, что он хочет, и как сделать, чтобы вышел именно шар? Как бы разгадав мысли Страшилы, Гудвин начал свой рассказ:
– Дорогой Страшила, всё дело в том, что портной сшивает не просто куски ткани, а вырезанные определённым образом лоскуты. Для этого он использует специальные трафареты, называемые выкройками. В зависимости от того, какую форму имеют эти выкройки и в какой последовательности сшиваются (что тоже очень важно), получается либо рубашка, либо брюки, либо ещё что-нибудь полезное. Аналогично можно поступить и для шара. Существует большое количество способов раскроить и сшить его. Предлагаю рассмотреть один из них. Ты видел когда-нибудь футбольный мяч?
– Конечно, видел, – ответил Страшила. – Так вот, – продолжал Гудвин, – обычно футбольный мяч шьют из кожи, используя для этого определённую выкройку. Части этой выкройки представляют собой правильные пяти- и шестиугольники…
– Правильные угольники? – прервал его Страшила. – Я что-то Вас совсем перестал понимать.
– Всё просто, – успокоил его Гудвин. – Правильные n-угольники – это вид геометрических фигур. Сейчас я всё объясню. Что такое отрезок прямой, ты себе представляешь? Отлично! Так вот, если сложить отрезки последовательно, то получится кривая, называемая ломаной. Соединив конец последнего звена с началом первого, её можно замкнуть…
– Прости меня, – снова прервал Страшила, – я думаю, что сам смогу всё узнать в библиотеке. Уж очень мне понравилось работать с литературой. Можно?
– Конечно! Иди в библиотеку и узнай всё сам. Встретимся завтра, – ответил Гудвин.
На следующий день Страшила принёс небольшой конспект.
Из конспекта Страшилы:
«…Ломаная называется простой, если каждое её звено имеет только одну общую точку с другим звеном. И эта точка является концом звена.
На рис. … изображены два типа ломаных. Ломаные, изображённые на рис. 5,а – простые.
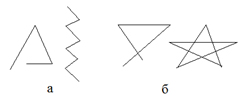
(Далее Страшила рассматривает только такой тип ломаных.)
Простая замкнутая ломаная разбивает плоскость на две области – внутреннюю и внешнюю относительно данной ломаной. Внешняя область обладает тем свойством, что в ней можно провести прямую, целиком принадлежащую данной области.
Простая замкнутая ломаная со всей внутренней областью называется многоугольником. При этом сама ломаная называется границей многоугольника. Звенья границы многоугольника – его стороны, а точки пересечения сторон – вершины многоугольника. Число вершин многоугольника равно числу его сторон.
Многоугольник называется выпуклым, если он целиком содержит отрезок, соединяющий две любые его точки, или если при продолжении любой из его сторон весь многоугольник лежит в одной полуплоскости относительно этой прямой. На рис. 6 многоугольники а) и б) – выпуклые, в) и г) – невыпуклые.
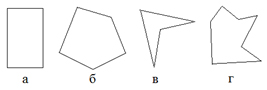
Выпуклый многоугольник называется правильным, если все его стороны равны…»
Гудвин был доволен конспектом.
– Теперь я понимаю, – радовался Страшила. – Многие вещи в природе и технике представляют собой правильные многоугольники. Например, пчелиные соты со стороны стенок имеют вид огромного числа правильных шестиугольников, скреплённых друг с другом. Я прочитал, что правильные шестиугольники обладают тем свойством, что ими можно устлать плоскость без промежутков. Этим свойством обладают и некоторые другие многогранники.
– Верно, – подтвердил Гудвин. – Однако, для нашего случая, более интересным можно считать свойство многоугольников в различных комбинациях образовывать поверхности, близкие к сферическим. Я уже говорил, приведя в пример футбольный мяч, что поверхность, близкую к шарообразной, можно скомбинировать из правильных пяти- и шестиугольников. В этом случае, правда, получается не сфера, а геометрическая фигура, называемая многогранником, грани которой образованы сшитыми многоугольниками. Но благодаря эластичности ткани (её способности тянуться) эта поверхность обладает шарообразной формой. Для наших же целей можно использовать более простые фигуры. Вот, смотри. (Рис. 7).
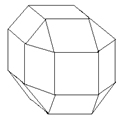
У этого многогранника 26 граней, 18 из них – квадраты, а остальные 8 – равносторонние треугольники. При том же объёме оболочки длина швов по сравнению с предыдущей конструкцией значительно меньше.
– Теперь можно начинать строить, – горел от нетерпения Страшила.
– Какой же ты нетерпеливый, – остудил Гудвин пыл своего друга. – Постройка любой модели – операция достаточно кропотливая. Надо всё точно рассчитать и проверить. Необходим план действий, сборочный чертёж, материал и многое другое. Вот, например, ты хочешь строить модель шара из парусины, а почему бы не выбрать для этого какой-нибудь иной материал? Конечно, она обладает рядом преимуществ перед другими материалами: прочная, плохо пропускает газ, хорошо держит достаточно высокие температуры. Всё это делает её отличным материалом для постройки больших воздушных шаров. Но я уже говорил, что любая модель не может обладать полной степенью адекватности (точности соответствия) с моделируемым объектом. В нашем случае причиной этого служит разница в размерах модели воздушного шара и его реального собрата. Посмотри, нагрузки, испытываемые моделью, во много раз меньше реальных, следовательно, фактор прочности отходит на второй план. С другой стороны, есть одна тонкость, которую сразу можно и не заметить. Если рассмотреть зависимость объёма и площади поверхности шара в зависимости от его радиуса,
V=4/3π r3, S=4π r2
то окажется, что V~S3/2, а это значит, что объём V «растёт быстрее» с увеличением радиуса r, чем площадь поверхности S. Так как подъёмная сила зависит от объёма оболочки, то при достаточно малых радиусах может оказаться, что материалы, подобные парусине, не пригодны для конструирования.
– Что же делать? – спросил Страшила. – Если парусина не подходит, то надо использовать какой-то другой материал?
– Да, именно так, – подтвердил Гудвин. – Предлагаю поступить так: я занимаюсь сборочными чертежами модели нашего шара, а ты тем временем пойдёшь в библиотеку и попытаешься подобрать подходящий материал.
Встретившись на следующий день, Гудвин и Страшила стали обмениваться накопленным опытом. И вот что у них получилось:
Материал для небольшой (диаметром до 1 м) модели воздушного шара может служить тонкая лавсановая плёнка, часто используемая для изготовления продуктовых пакетов, либо аналогичная ей плёнка из лёгкого материала. Лавсан достаточно прочен и, в отличие от полиэтилена, несильно коробится при кратковременном воздействии достаточно высоких температур, плохо тянется. Это высокотехнологичный материал. Лавсан хорошо склеивается универсальными клеями типа «Момент» и «Суперцемент» (первый предпочтительнее в силу быстрого затвердевания). Для постройки шара больших размеров можно использовать более толстые лавсановые плёнки или папиросную бумагу.
Основные части выкройки модели имеют следующий вид (рис. 8):
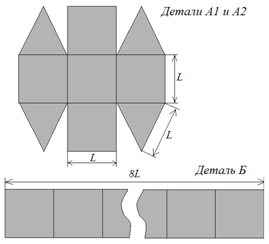
Если нет достаточно больших кусков лавсановой плёнки, то каждую из этих частей, в свою очередь, можно склеить из квадратов и равносторонних треугольников, соединяя их по пунктирным линиям, как указано на чертеже.
Для этого при раскрое плёнки необходимо оставлять припуски для швов по 0,5 см от каждого края. Припуски специально делаются небольшими: лишний материал значительно увеличивает вес всей конструкции.
Особое внимание при склеивании нужно уделять местам угловых стыков деталей. Это – самые ответственные места. В них могут оставаться дыры, в которые потом будет уходить нагретый воздух.
Склейку проще всего производить вдвоём: один держит склеиваемые детали за края, а второй смазывает швы клеем и плотно прижимает их. При склеивании надо стараться, чтобы плёнка не коробилась и не мялась. Последнее очень важно для герметичности оболочки.
Прежде чем склеивать детали А1 и А2 выкройки оболочки, в соединяющей их ленте Б необходимо, в соответствии с чертежом, проделать отверстие под горелку (рис. 9).
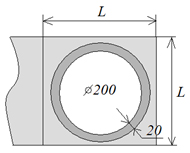
Для жёсткости края отверстия укрепляются двумя кольцами из тонкого картона, которые наклеиваются на наружной и внутренней сторонах оболочки по периметру отверстия. К ним на трёх проволочках крепится горелка, изготавливаемая из фольги. Диаметр горелки – 5 см. В качестве горелки можно использовать крышку от бутылки с кефиром или ряженкой. Для большого шара хорошей горелкой служит дно от банки из-под «Пепси-Колы» (рис. 10).
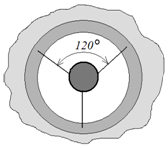
Так же к картонному кольцу на четырёх нитках крепится и корзина, в качестве которой можно использовать бумажный куб без одной грани со стороной 2-2,5см.
После сборки необходимо ещё раз убедиться в герметичности оболочки шара и устранить все найденные отверстия.
Масса получившейся конструкции не должна превышать 25-30 грамм.
Топливом для модели служит сухое горючее, продающееся в хозяйственных и спортивных магазинах.
Запуск шара производится в следующем порядке:
На открытом воздухе шар поднимается на несколько сот метров. Отпускать шар в свободный полёт опасно, так как горелка может поджечь окружающие предметы и здания. Поэтому к корзине точно посередине необходимо прикрепить леер из толстой нитки. Кроме того, даже лёгкий ветер очень далеко сносит шар, и есть вероятность, что вы его просто не найдёте.
Нельзя запускать шар при сильном ветре. Резкий порыв может накренить оболочку, что приведёт к её возгоранию.
Когда горючее прогорит, и температура воздуха в оболочке уменьшится, шар начнёт садиться. При посадке шар необходимо принимать в руки и поддерживать его в вертикальном положении до остывания горелки, чтобы избежать возможности его возгорания.

| Сохранить для печати |
|---|